



Next: Approximation en loi de
Up: Comptages de sources, rayonnement
Previous: Comptages dans le cas
Dans un Univers en expansion, trois effets affectent fortement le nombre de sources par stéradian pour une densité de flux donnée:
- le nombre de sources est plus petit par effet de courbure dans la géométrie non euclidienne que dans le cadre de la géométrie euclidienne
- le redshift, qui décale la fréquence d'observation par rapport à la fréquence d'émission, peut affecter la luminosité apparente de la source si son spectre varie fortement avec la fréquence
- les sources distantes, plus jeunes que les sources locales, introduisent des effets d'évolution
Dans un Univers en expansion, S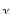 est donné par:
est donné par:
S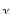 = = 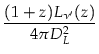
|
(4.10) |
où z est le redshift de la source, 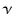 est la fréquence d'observation,
est la fréquence d'observation, 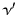 est la fréquence d'émission, avec
est la fréquence d'émission, avec
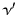 =
= 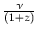 .
L
.
L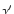 (z) est la luminosité de la source à la fréquence
(z) est la luminosité de la source à la fréquence 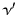 à l'époque correspondant au redshift z. DL est la distance de luminosité, donnée par:
à l'époque correspondant au redshift z. DL est la distance de luminosité, donnée par:
DL(z) = 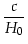 ![$\displaystyle {\frac{z q_0 + (1 - q_0)\left [1 - (1 + 2 z q_0) ^{1/2} \right ] }{q_0^2}}$](img121.gif)
|
(4.11) |
où H0 est la constante de Hubble, q0 le paramètre de décélération.
Par souci de simplification d'écriture, nous intoduisons la fonction f (z) (que nous utiliserons dans le cadre de la modélisation):
où
RH = cH0-1 est le rayon de Hubble.
Je rappelle que q0 vaut
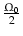 -
- 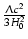 , où
, où 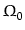 est le paramètre de densité,
est le paramètre de densité, 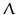 la constante cosmologique, et c la célerité de la lumière.
la constante cosmologique, et c la célerité de la lumière.
En introduisant dans l'équation 4.10 les rapports
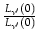 et
et
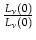 , nous obtenons:
, nous obtenons:
qui peut se réécrire sous la forme:
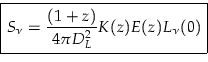
|
(4.14) |
Le rapport
K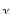 (z) =
(z) = 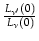 , est la correction-K. Elle indique comment varie le spectre de la source: observée à la fréquence
, est la correction-K. Elle indique comment varie le spectre de la source: observée à la fréquence 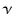 , l'effet de redshift explore son spectre aux fréquences inférieures
, l'effet de redshift explore son spectre aux fréquences inférieures
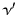 =
= 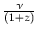 . Des exemples de corrections-K pour les fréquences observées par ISO ont été présentées en figure 2.11, et utilisent les spectres de galaxie présentés en figure 5.2.
. Des exemples de corrections-K pour les fréquences observées par ISO ont été présentées en figure 2.11, et utilisent les spectres de galaxie présentés en figure 5.2.
Le rapport
E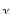 (z) =
(z) = 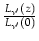 , appelé correction-E, explicite l'effet d'évolution de la luminosité avec le redshift. La source observée à un redshift z est d'autant plus jeune que z est grand, donc E est sensible à l'évolution en luminosité. On peut aussi définir une évolution en nombre qui décrit le changement du nombre de sources pour une luminosité donnée en fonction du redshift.
, appelé correction-E, explicite l'effet d'évolution de la luminosité avec le redshift. La source observée à un redshift z est d'autant plus jeune que z est grand, donc E est sensible à l'évolution en luminosité. On peut aussi définir une évolution en nombre qui décrit le changement du nombre de sources pour une luminosité donnée en fonction du redshift.
La densité de flux devient:
S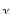 = = 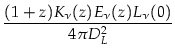
|
(4.15) |
Le nombre de sources dN observées dans l'angle solide d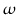 avec des flux compris entre S
avec des flux compris entre S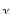 et
S
et
S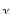 + dS
+ dS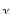 est:
est:
dN = 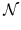 (z)dV(z) (z)dV(z)
|
(4.16) |
où
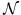 (z) est physiquement le nombre de sources de luminosités comprises entre
L
(z) est physiquement le nombre de sources de luminosités comprises entre
L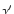 (z) et
L
(z) et
L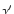 (z) + dL
(z) + dL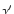 (z), reliés à S
(z), reliés à S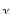 selon l'équation 4.10. On obtient:
selon l'équation 4.10. On obtient:
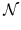 (z) = (z) = 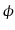 (z, L (z, L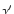 (z))(1 + z)3dL (z))(1 + z)3dL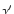 (z) (z)
|
(4.17) |
et où
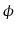 (z, L
(z, L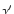 (z)) est la densité comobile au redshift z pour la luminosité
L
(z)) est la densité comobile au redshift z pour la luminosité
L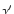 (z).
(z).
L'élément de volume dV(z) au redshift z est donné par:
dV(z) = RHDA2(z)g(z)d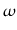 dz dz
|
(4.18) |
où le temps propre t est relié au redshift z via:
- c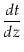 = = 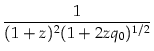 = g(z)RH = g(z)RH
|
(4.19) |
et où la distance angulaire DA(z) est reliée à la distance de luminosité DL(z) par:
DA(z) = 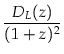
|
(4.20) |




Next: Approximation en loi de
Up: Comptages de sources, rayonnement
Previous: Comptages dans le cas
Dr Hervé Dole, University of Arizona, http://mips.as.arizona.edu/~hdole
Mon 05-Feb-2001 16:58 PST
![]() est donné par:
est donné par:
![]() -
- ![]() , où
, où ![]() est le paramètre de densité,
est le paramètre de densité, ![]() la constante cosmologique, et c la célerité de la lumière.
la constante cosmologique, et c la célerité de la lumière.
![]() et
et
![]() , nous obtenons:
, nous obtenons:
![]() (z) =
(z) = ![]() , est la correction-K. Elle indique comment varie le spectre de la source: observée à la fréquence
, est la correction-K. Elle indique comment varie le spectre de la source: observée à la fréquence ![]() , l'effet de redshift explore son spectre aux fréquences inférieures
, l'effet de redshift explore son spectre aux fréquences inférieures
![]() =
= ![]() . Des exemples de corrections-K pour les fréquences observées par ISO ont été présentées en figure 2.11, et utilisent les spectres de galaxie présentés en figure 5.2.
. Des exemples de corrections-K pour les fréquences observées par ISO ont été présentées en figure 2.11, et utilisent les spectres de galaxie présentés en figure 5.2.
![]() (z) =
(z) = ![]() , appelé correction-E, explicite l'effet d'évolution de la luminosité avec le redshift. La source observée à un redshift z est d'autant plus jeune que z est grand, donc E est sensible à l'évolution en luminosité. On peut aussi définir une évolution en nombre qui décrit le changement du nombre de sources pour une luminosité donnée en fonction du redshift.
, appelé correction-E, explicite l'effet d'évolution de la luminosité avec le redshift. La source observée à un redshift z est d'autant plus jeune que z est grand, donc E est sensible à l'évolution en luminosité. On peut aussi définir une évolution en nombre qui décrit le changement du nombre de sources pour une luminosité donnée en fonction du redshift.
![]() avec des flux compris entre S
avec des flux compris entre S![]() et
S
et
S![]() + dS
+ dS![]() est:
est: