



Next: Comptages FIRBACK
Up: Résultats: comptages à 170 m
Previous: Correction de complétude
Figure 4.25:
Simulation du biais de Malmquist-Eddington dans un diagramme
de comptages différentiels. Les courbes verticales en tiret
indiquent les flux correspondant á 3, 4, et
5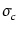 . La
droite noire représente le modèle d'entrée des comptages
différentiels en loi de puissance 3.3 avec coupure á
0.1
. La
droite noire représente le modèle d'entrée des comptages
différentiels en loi de puissance 3.3 avec coupure á
0.1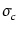 . La courbe rouge représente les comptages observés
lorsqu'une incertitude dans la photométrie est introduite. Les
points avec barre d'erreur sont les comptages FIRBACK non corrigés de cet
effet. Ils sont ajustés par les observations simulées. Après la
correction, ils sont donc ajustés par le modèle d'entrée. Les
tirets verticaux indiquent respectivement 1, 3, 4 et
5
. La courbe rouge représente les comptages observés
lorsqu'une incertitude dans la photométrie est introduite. Les
points avec barre d'erreur sont les comptages FIRBACK non corrigés de cet
effet. Ils sont ajustés par les observations simulées. Après la
correction, ils sont donc ajustés par le modèle d'entrée. Les
tirets verticaux indiquent respectivement 1, 3, 4 et
5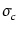 .
.
|
|
Figure 4.26:
Correction du biais de Malmquist-Eddington en fonction du
flux sur la pente des comptages. La correction est de l'ordre de 20%
(resp 30%) à
5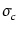 (resp.
4
(resp.
4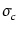 ).
).
|
|
L'incertitude sur la détermination des flux provoque, dans les
comptages de sources, un accroissement artificiel de la pente. En
effet, une source de flux S peut être mesurée au flux
S + 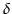 S
ou
S -
S
ou
S - 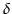 S. Puisque les sources faibles sont plus nombreuses
que les sources fortes, on observera statistiquement plus de sources
faibles de flux S observées en fait au flux
S +
S. Puisque les sources faibles sont plus nombreuses
que les sources fortes, on observera statistiquement plus de sources
faibles de flux S observées en fait au flux
S + 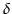 S.
Le phénomène s'intensifie à la coupure en flux du catalogue: des
sources en principe non retenues, car de flux S en deçà du seuil Scut
du catalogue, peuvent être prise en compte á cause des
incertitudes de photométrie et ainsi être mesurées à
S +
S.
Le phénomène s'intensifie à la coupure en flux du catalogue: des
sources en principe non retenues, car de flux S en deçà du seuil Scut
du catalogue, peuvent être prise en compte á cause des
incertitudes de photométrie et ainsi être mesurées à
S + 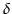 S > Scut. Cet effet est connu sous le nom de biais de
Malmquist-Eddington [Theureau et al.(1997),Teerikorpi(1998), par exemple].
S > Scut. Cet effet est connu sous le nom de biais de
Malmquist-Eddington [Theureau et al.(1997),Teerikorpi(1998), par exemple].
J'ai effectué des simulations sur des comptages différentiels. Sur
un modèle de comptages d'entrée (en loi de puissance 3.3), je simule l'effet d'une
observation en introduisant une incertitude dans les
flux. Techniquement, il s'agit d'effectuer la convolution de la courbe
des comptages d'entrée avec une gaussienne d'écart-type
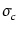 , le bruit de confusion. Cette technique a l'avantage
d'être simple à mettre en oeuvre, mais fait l'approximation que
l'incertitude sur les flux est constante. Nous avons vu que ce n'est
pas le cas (cf. section 4.6.3), mais le biais
domine aux faibles flux, typiquement inférieurs à
4
, le bruit de confusion. Cette technique a l'avantage
d'être simple à mettre en oeuvre, mais fait l'approximation que
l'incertitude sur les flux est constante. Nous avons vu que ce n'est
pas le cas (cf. section 4.6.3), mais le biais
domine aux faibles flux, typiquement inférieurs à
4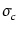 ,
dans un régime où
,
dans un régime où 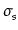 est quasi constant et de l'ordre du
bruit de confusion.
est quasi constant et de l'ordre du
bruit de confusion.
La figure 4.25 montre la simulation du biais en fonction du
flux, dans un diagramme de comptages différentiels. La figure
4.26 montre le rapport entre les comptages
d'entrée et les comptages observés en simulation, et donne la
valeur de la correction à apporter. Noter que la correction ne varie pas
de plus de 5% (resp 10%)
à
5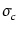 (resp.
4
(resp.
4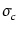 ) en fonction de la loi de puissance
des comptages d'entrée dans le domaine 3.0 - 3.6.
) en fonction de la loi de puissance
des comptages d'entrée dans le domaine 3.0 - 3.6.
Figure 4.27:
Comptages différentiels FIRBACK.
|
|
Figure 4.28:
Comptages intégraux FIRBACK: rond noir: comptages sur tout le relevé; losanges: comptages préliminaires FIRBACK sur FSM1 de [Puget et al.(1999)]; étoile: point de [Kawara et al.(1998)].
|
|




Next: Comptages FIRBACK
Up: Résultats: comptages à 170 m
Previous: Correction de complétude
Dr Hervé Dole, University of Arizona, http://mips.as.arizona.edu/~hdole
Mon 05-Feb-2001 16:58 PST
![\includegraphics[width=0.7\textwidth]{Chap4/edd1.eps}](img230.gif)
![\includegraphics[width=0.7\textwidth]{Chap4/edd1.eps}](img230.gif)
![\includegraphics[width=0.8\textwidth]{Chap4/eddington_malmquist_counts.eps}](img231.gif)
![]() , le bruit de confusion. Cette technique a l'avantage
d'être simple à mettre en oeuvre, mais fait l'approximation que
l'incertitude sur les flux est constante. Nous avons vu que ce n'est
pas le cas (cf. section 4.6.3), mais le biais
domine aux faibles flux, typiquement inférieurs à
4
, le bruit de confusion. Cette technique a l'avantage
d'être simple à mettre en oeuvre, mais fait l'approximation que
l'incertitude sur les flux est constante. Nous avons vu que ce n'est
pas le cas (cf. section 4.6.3), mais le biais
domine aux faibles flux, typiquement inférieurs à
4![]() ,
dans un régime où
,
dans un régime où ![]() est quasi constant et de l'ordre du
bruit de confusion.
est quasi constant et de l'ordre du
bruit de confusion.
![]() (resp.
4
(resp.
4![]() ) en fonction de la loi de puissance
des comptages d'entrée dans le domaine 3.0 - 3.6.
) en fonction de la loi de puissance
des comptages d'entrée dans le domaine 3.0 - 3.6.
![\includegraphics[width=0.95\textwidth]{Chap4/counts_alone_diff.eps}](img232.gif)
![\includegraphics[width=0.95\textwidth]{Chap4/counts_alone.eps}](img233.gif)